Forleden havde vi i foreningen besøg af en Swarovski repræsentant, der energisk og engageret fortalte om Swarowskis produktion af kikkerter og linsesystemer.

Moderne kikkerter er nu forsynet med tårne, hvorpå man kan klikke og indstille således, at man ikke selv behøver at tænke på, hvordan det nu er, når man f.eks. skal skyde på en vinkel 60gr opad eller nedad.

Der kom fra forsamlingen kom netop et spørgsmål desangående: Hvorfor skal man holde lavt ved skydning på stejle vinkler, eller hvordan er det?

Det gav anledning til en del diskussion blandt de fremmødte.

Svaret fra repræsentanten var, ”at man skal holde lavt, fordi tyngdekraften er en anden, ændrer sig, når man skyder opad eller nedad”.

At man skal holde lavt er korrekt, men forklaringen er helt forkert. Tyngdekraften er naturligvis den samme, hvad enten man skyder opad eller nedad! Eller vandret for den sags skyld. 

Tyngdekraften afhænger kun af massen (som én af tilhørerne ganske rigtigt bemærkede) og kan beregnes som tyngdeaccelerationen gange med massen.

Det gik jeg i pausen også op og sagde diskret til ham, hvad han også indrømmede, men så kom han ikke rigtig mere ind på det.

I anden anledning har jeg på tryk læst ”at tyngdekraften kun virker på bevægelse i vandret retning”, hvilket naturligvis også er helt forkert. Ellers ville ting, der kastes lodret i vejret, jo aldrig komme ned igen. 

Og hvordan er det desuden, når man fra et tårn skal skyde på et stykke vildt, der står næsten lige neden for skydestigen/tårnet? Skal man holde højt eller lavt på dyret?

Lad os først se på vandret skydning, den retning som vi normalt indskyder på:

Et projektil, en baneretning og en tyngdekraft, som virkerlodret nedad mod jorden:

Bemærk, at lige i begyndelsen af projektilets bane, virker tyngdekraften vinkelret på banen. Senere ændrer vinklen sig: Banens retning er mere og mere nedad, men tyngdekraftener stadig lige nedad, og har samme størrelse dvs. man skal tegne pilen med samme længde:                                  

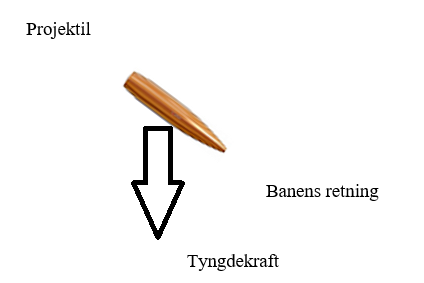
og til sidst rammer projektilet naturligvis jorden.

Vi kigger nu på en bane, der er rettet mod et højtliggende punkt (f.eks. på et bjerg):

Tyngdekraften kan nu betragtes som bestående af to dele 

1) en del som er vinkelret på projektilet P 

2) en del som er langs med projektilet, og modsat rettet dette L 

Dvs. man kan danne et rektangel, hvor de to nye pile er siderne og tyngdekraften er diagonal. De to nye pile kan ”erstatte” tyngdekraften..

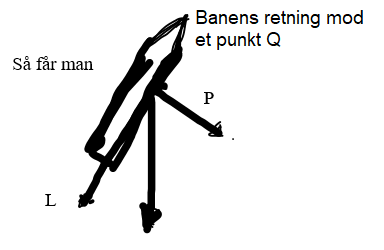
Nu er det kun P (den vinkelrette del) der bevirker at projektilet afbøjes mod jorden og den del af tyngdekraften er meget jo meget mindre end selve tyngdekraften, eller med andre ord, projektilet når ikke at falde så meget mod jorden som ved vandret skydning.

Holder man så, som ved vandret skydning, ja så rammer man over målet  

Konklusion:

Man skal således holde under målet, altså lavt. Skyder man nu nedad, ja så får man ved nøjagtig samme fremgangsmåde: Den del af tyngdekraften, der bevirker afbøjningen, bliver mindre!

Et godt tysk mundheld: Berg herauf und berg herunter, immer halt drunter! 

Man skal således holde på målet svarende til den vandrette afstand hen til punktet Q Denne afstand afhænger af vinklen man skyder på og afstanden op til punktet Q og kan nemt beregnes. De beregningers resultater er der tabeller over, og de ligger i programmer, som kan købes og lægges i tårnene på kikkerten.

Men når man skyder fra tårn på et dyr som står næsten lige for skydestigen, skal man holde højt! På den korte afstand får de tyngdekraftsforhold, som er beskrevet ovenfor, ingen betydning. Men den korte afstand får her betydning. Vi følger sigtelinien gennem kikkerten, og det er jo den, man har indskudt sin riffel efter. Men centerlinien fra riffelen ligger jo under sigtet fra kikkerten. Holder man så på bladet på siden af dyret, går projektilet jo for lavt, og projektilet kan gå under dyret. Man skal derfor løfte riflen dvs. holde højt! Der er naturligvis andre kræfter, der påvirker projektilet, f.eks luftmodstand som har samme retning som L på tegningen, men er langt større end L, som så og sige ingen betydning har. Og der er kræfter fra vinden og kræfter der skyldes projektilets projektion, og andre. Men jeg har her koncentreret mig om forholdene vedrørende stejlskydning.